компютърен компонент - онлайн пъзели




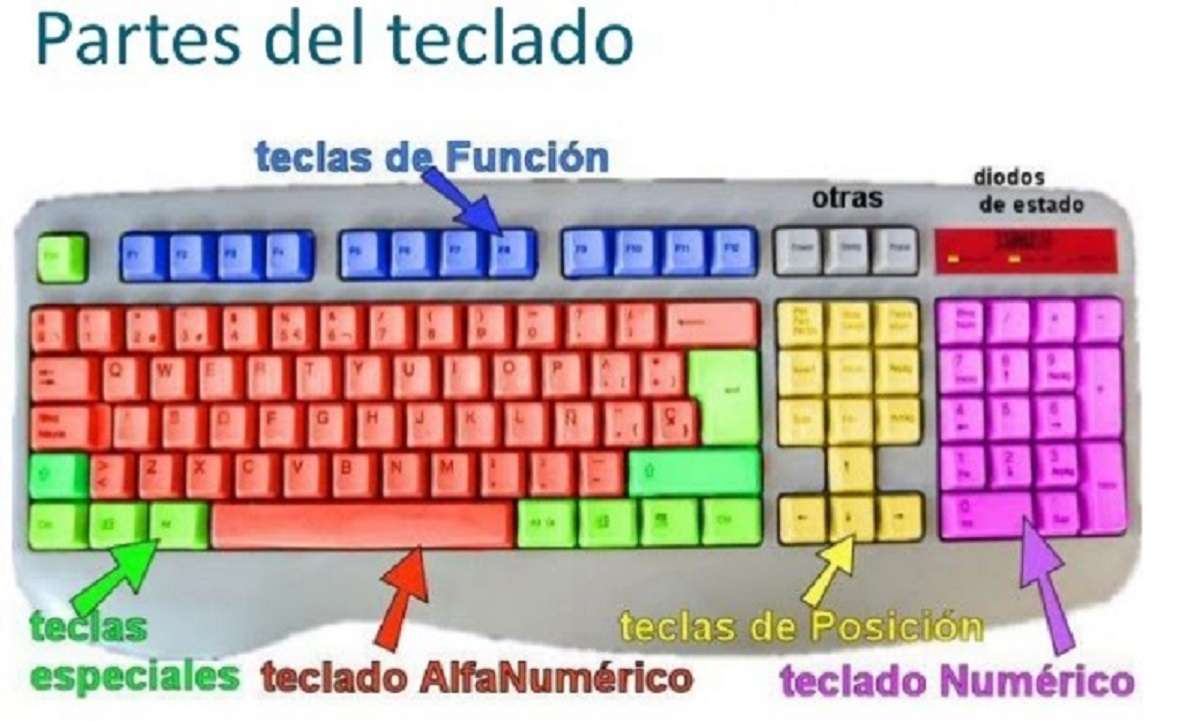







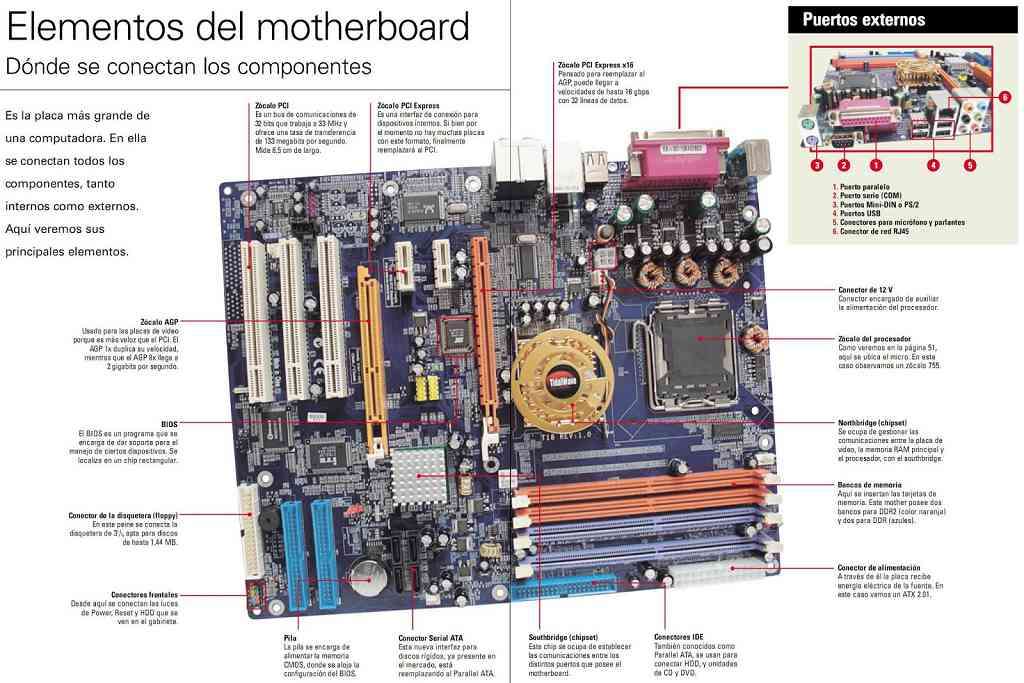

































Онлайн пъзел компютърен компонент
В числения анализ, методът на крайните елементи е удобен инструмент за числено решаване на частни диференциални уравнения. Такива уравнения често описват динамиката на разнообразни механични, термодинамични, акустични и други физични системи.
По-конкретно, този метод позволява да се моделира числено поведението на сложни системи, при условие че се разглеждат като непрекъснати среди и динамиката им се описва с линейни частни диференциални уравнения: например, движението на струна, фиксирана за един от краищата си, динамиката на флуид, връхлитащ с голяма скорост препятствие, деформация на метални структури и др.
Въведение
Методът на крайните елементи е част от инструментариума на приложната математика. Целта му е чрез методи, пренесени от вариационното смятане, да се изработи дискретен алгоритъм, чрез който да бъде намерено приближено решение на частно диференциално уравнение (ЧДУ) в компактен интервал с дадени гранични условия. В зависимост от дадени граничните условия, задачата се нарича Проблем на Дирихле (дадени са стойностите на функцията на границите на интервала), на Нюман (когато са дадени стойностите на градиента на функцията) или на Робин (когато е дадена връзка между градиента и стойностите на функцията).
Както и други методи за приближено решаване на ЧДУ и при метода на крайните елементи трябва да се отделя особено внимание на евентуалните проблеми, свързани с дискретизацията на интервала, в който се търси решението, като:
Съществуването на решение
Единственост на откритото решение
Стабилност
Сходимост
и най-вече, изработване на критерии за сравнение на полученото чрез дискретизация решение с пълното решение.
Основен принцип
Методът на крайните елементи позволява да се реши, чрез дискретизация, частно диференциално уравнение, за което се търси достатъчно „благонадеждно“ решение. В общия случай, това уравнение свързва частните производни да дадена функция u, дефинирана в даден интервал. За съществуването на решение на проблема и за неговата единственост е необходимо да са дадени граничните условия.