componente del computer - puzzle online




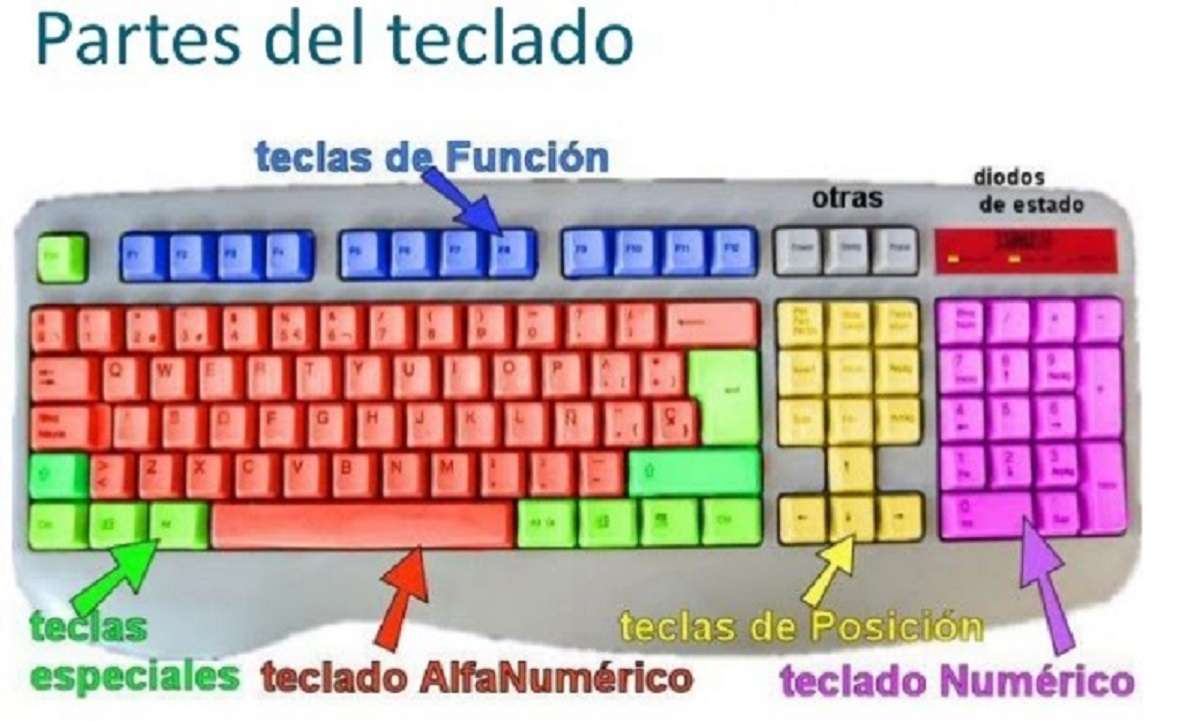




























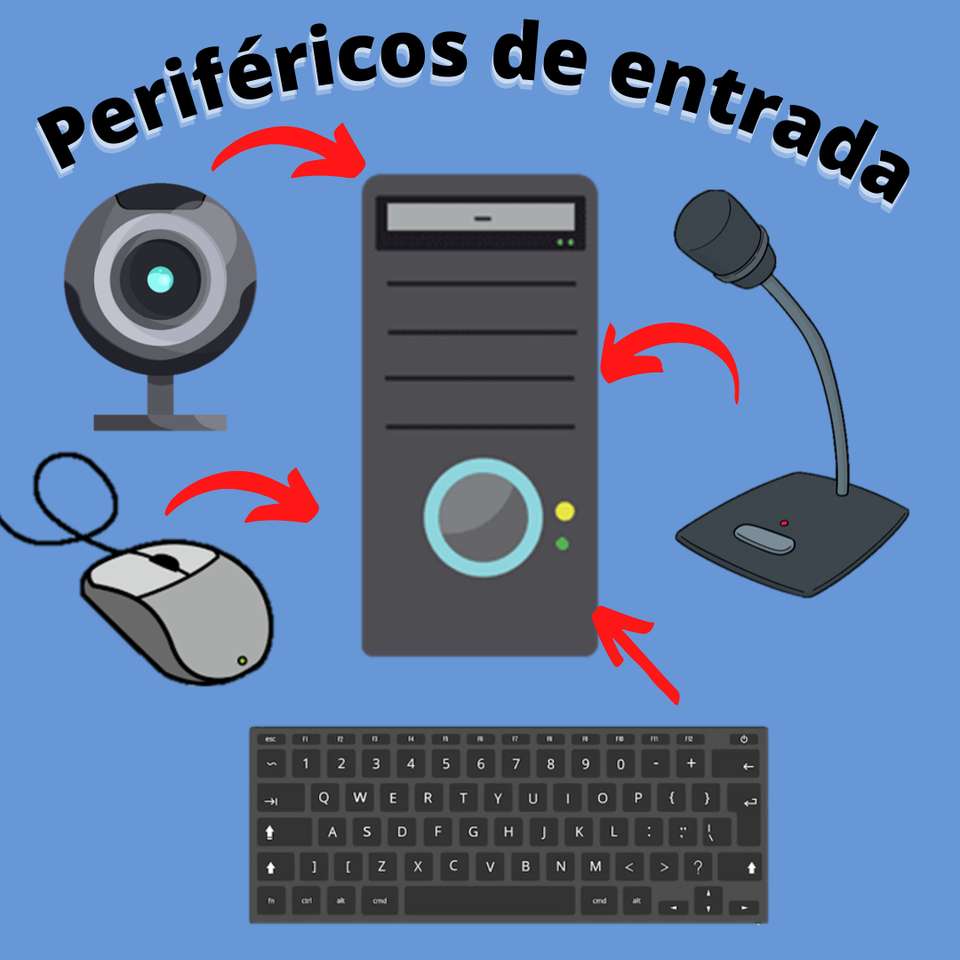



















Puzzle online componente del computer
In matematica, il metodo degli elementi finiti (FEM, dall'inglese Finite Element Method) è una tecnica numerica atta a cercare soluzioni approssimate di problemi descritti da equazioni differenziali alle derivate parziali riducendo queste ultime ad un sistema di equazioni algebriche.
Benché esso competa in alcuni ambiti limitati con altre strategie numeriche (metodo delle differenze finite, metodo dei volumi finiti, metodo degli elementi al contorno, metodo delle celle, metodo spettrale, etc.), il metodo FEM mantiene una posizione dominante nel panorama delle tecniche numeriche di approssimazione e rappresenta il kernel di gran parte dei codici di analisi automatici disponibili in commercio.
In generale, il metodo agli elementi finiti si presta molto bene a risolvere equazioni alle derivate parziali quando il dominio ha forma complessa (come il telaio di un'automobile o il motore di un aereo ), quando il dominio è variabile (per esempio una reazione a stato solido con condizioni al contorno variabili), quando l'accuratezza richiesta alla soluzione non è omogenea sul dominio (in un crash test su un autoveicolo, l'accuratezza richiesta è maggiore in prossimità della zona di impatto) e quando la soluzione cercata manca di regolarità. Inoltre, il metodo è alla base dell'analisi agli elementi finiti.
Cenni storici
Il metodo degli elementi finiti trova origini nelle necessità di risoluzione di problemi complessi di analisi elastica e strutturale nel campo dell' ingegneria civile ed aeronautica. I primordi del metodo possono essere fatti risalire agli anni 1930 -35 con i lavori di A. R. Collar e W. J. Duncan, che introducono una forma primitiva di elemento strutturale nella risoluzione di un problema di aeroelasticità, e agli anni 1940 -41 con i lavori di Alexander Hrennikoff e Richard Courant, dove entrambi, benché in differenti approcci, condividevano l' idea di suddividere il dominio del problema in sottodomini di forma semplice (gli elementi finiti).Tuttavia la nascita vera e propria e lo sviluppo del metodo agli elementi finiti si colloca nella seconda metà degli anni '50 con il contributo fondamentale di M. J. (Jon) Turner della Boeing, che formulò e perfezionò il Direct Stiffness Method, il primo approccio agli elementi finiti nel campo del continuo. Il lavoro di Turner trovò diffusione fuori dagli stretti ambiti dell' ingegneria aerospaziale, ed in particolare nell' ingegneria civile, tramite il lavoro di John Argyris presso l' Università di Stoccarda (che negli stessi anni aveva proposto una unificazione formale del metodo delle forze e del metodo degli spostamenti sistematizzando il concetto di assemblaggio delle relazioni di un sistema strutturale a partire dalle relazioni degli elementi componenti), e di Ray W. Clough presso l' Università di Berkeley (che parlò per primo di metodo FEM e la cui collaborazione con Turner aveva dato vita al celebre lavoro, considerato come l'inizio del moderno FEM).
Altri contributi fondamentali alla storia dei FEM sono quelli di B. M. Irons, cui sono dovuti gli elementi isoparametrici, il concetto di funzione di forma, il patch test ed il frontal solver (un algoritmo per la risoluzione del sistema algebrico lineare), di R. J. Melosh, che inquadrò il metodo FEM nella classe dei metodi Rayleigh-Ritz e sistematizzò la sua formulazione variazionale (una rigorosa e famosa esposizione della basi matematiche del metodo fu anche fornita nel 1973 da Strang e Fix) e di E. L.Wilson, che sviluppo il primo (e largamente imitato) software FEM open source che diede genesi al SAP.Nel 1967 Zienkiewicz pubblicò il primo libro sugli elementi finiti. A partire dagli anni '70, il metodo FEM ha trovato diffusione come strategia di modellazione numerica di sistemi fisici in un'ampia varietà di discipline ingegneristiche, per esempio elettromagnetismo, fluidodinamica, calcolo strutturale e geotecnica. Sempre negli anni nacquero gran parte dei codici di analisi FEM commerciali (NASTRAN, ADINA, ANSYS, ABAQUS, SAMCEF, MESHPARTS, etc) tuttora disponibili.