composant informatique - puzzles en ligne











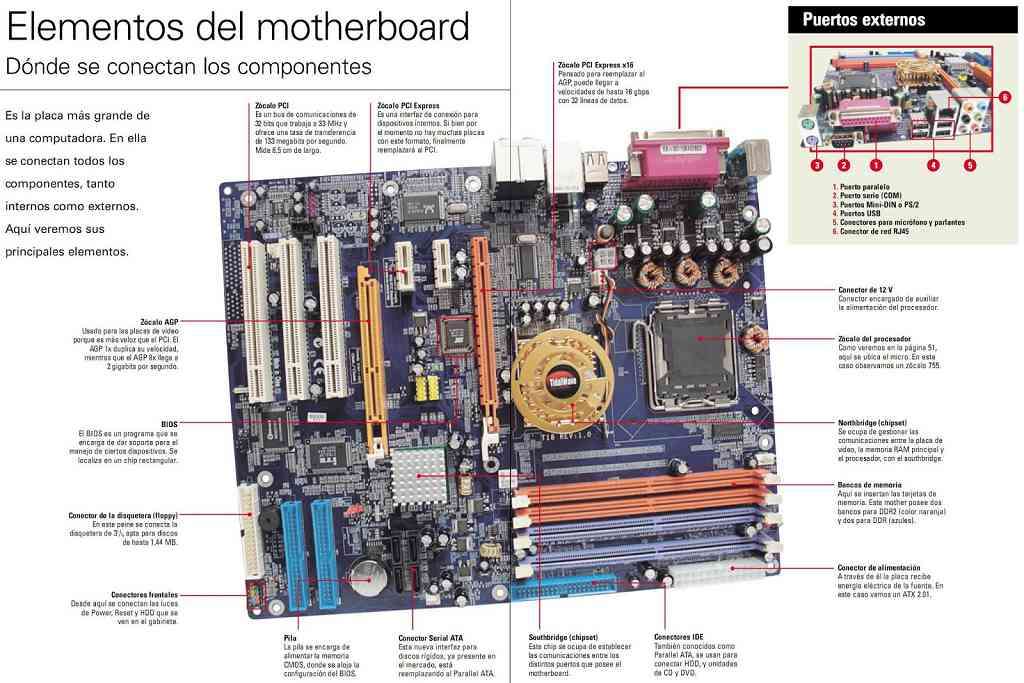

































Puzzle en ligne composant informatique
En analyse numérique, la méthode des éléments finis (MEF, ou FEM pour finite element method en anglais) est utilisée pour résoudre numériquement des équations aux dérivées partielles. Celles-ci peuvent par exemple représenter analytiquement le comportement dynamique de certains systèmes physiques (mécaniques, thermodynamiques, acoustiques, etc.).
Concrètement, cela permet par exemple de calculer numériquement le comportement d'objets même très complexes, à condition qu'ils soient continus et décrits par une équation aux dérivées partielles linéaire : mouvement d'une corde secouée par l'un de ses bouts, comportement d'un fluide arrivant à grande vitesse sur un obstacle, déformation d'une structure métallique, etc.
Introduction
La méthode des éléments finis fait partie des outils de mathématiques appliquées. Il s'agit de mettre en place, à l'aide des principes hérités de la formulation variationnelle ou formulation faible, un algorithme discret mathématique permettant de rechercher une solution approchée d’une équation aux dérivées partielles (ou EDP) sur un domaine compact avec conditions aux bords et/ou dans l' intérieur du compact. On parle couramment de conditions de type Dirichlet (valeurs aux bords) ou Neumann (gradients aux bords) ou de Robin (relation gradient/valeurs sur le bord ).
Il s'agit donc avant tout de la résolution approchée d'un problème, où, grâce à la formulation variationnelle, les solutions du problème vérifient des conditions d' existence plus faibles que celles des solutions du problème de départ et où une discrétisation permet de trouver une solution approchée. Comme de nombreuses autres méthodes numériques, outre l' algorithme de résolution en soi, se posent les questions de qualité de la discrétisation :
existence de solutions ;
unicité de la solution ;
stabilité ;
convergence ;
et bien sûr : mesure d'erreur entre une solution discrète et une solution unique du problème initial.La partie 2 va présenter le cadre général de la méthode des éléments finis, ainsi que le cas pratique le plus courant considérant des équations aux dérivées partielles linéaires dont on cherche une approximation par des fonctions affines.
La présentation en partie 3 est essentiellement physique, notamment mécanique. Elle ne doit être considérée que comme une présentation des éléments constitutifs de la modélisation discrète utilisée en résistance des matériaux via la méthode des éléments finis.